Music theory in F# - Major scale
This is the second part of the music theory in F# series:
- Introduction
- Step 1: Random note
- Step 2: The Major scale
- Step 3: Chords of the Major scale
Theory
There are 12 notes in an octave, but if I play random notes, the sound of the melody will be closer to a piano falling down the stairs than a Beethoven sonata. Fortunately, scales will help us.
The most famous scale is the major scale. A scale has a starting note named root and other notes after it. In example the C major scale is:
C, D, E, F, G, A, B
A scale is defined by the intervals between each notes. To create a major scale, choose a root note and add these intervals:
Whole tone, semitone, whole tone, whole tone, whole tone, semitone
For instance, to create a C major:
Root: C
Second: D = C + 2 semitones
Third: E = D + 2 semitones
Fourth: F = E + 1 semitone
Fifth: G = F + 2 semitones
Sixth: A = G + 2 semitones
Seventh: B = A + 2 semitones
Octave: C = B + 1 semitone
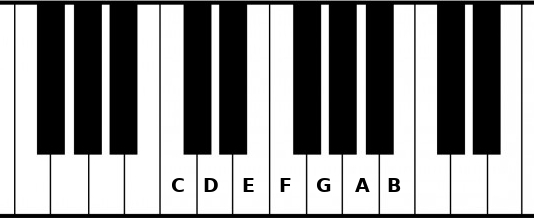
Each note of the scale is named after its position (root, second, third…). You can now create any major scale by applying these intervals. Here is another example, E major:
Root: E
Second: F# = E + 2 semitones
Third: G# = F# + 2 semitones
Fourth: A = G# + 1 semitone
Fifth: B = A + 2 semitones
Sixth: C# = B + 2 semitones
Seventh: D# = C# + 2 semitones
Octave: E = D# + 1 semitone
And so on…
Code
We can start by designing the MajorScale type and its module.
type MajorScale = MajorScale of Note
module MajorScale =
let private intervals = [ 2; 2; 1; 2; 2; 2; 1 ]
Remember the union type for the Note type? It can be seen as an enum, but unions are more than that because each case can have its own data:
type Shape =
| Point
| Square of int
| Rectangle of int * int // int * int is the type for a tuple of int and int
// All these values are Shape
let point = Point
let square = Square 3
let rect = Rectangle (4, 5) // (4, 5) is a value for a tuple of int and int
Well, MajorScale is a single union. It’s a trick to wrap a type into another one with a clear intention. More explanations in this article.
Now we want a notes function that takes a MajorScale and return the list of its Notes. In the theory part, we saw that the algorithm to find all the notes behave like this:
Return the root note
foreach interval in intervals
return the previous note + interval
This function already exists, it is called List.scan. It takes 3 parameters:
- The list to iterate (
intervals) - The starting point (
root note) - The function to compute the new value from the current item and the previous value (
previous note+interval)
module MajorScale =
let private intervals = [ 2; 2; 1; 2; 2; 2; 1 ]
let notes (MajorScale root) =
let addSemitones note interval = // not implemented yet
intervals
|> List.scan addSemitones root
// expected behavior
let cMajorNotes = MajorScale C |> notes // [ C; D; E; F; G; A; B ]
The function notes takes a MajorScale as parameter and destructures it. By doing this, we can easily access to root of the scale.
Then addSemitones is a function that takes a note and an interval and return the new note:
// expected behavior
let dSharp = addSemitones D 1 // DSharp
With this function implemented, notes called on a MajorScale C will return:
[ C; D; E; F; G; A; B; C ]
C appears two times because the last interval 1 is the interval from the seventh to the octave. We don’t need it to get all the notes, so we can remove the last interval:
module MajorScale =
let private intervals = [ 2; 2; 1; 2; 2; 2; 1 ]
let notes (MajorScale root) =
let addSemitones note interval = // not implemented yet
intervals
|> List.take (intervals.Length - 1)
|> List.scan addSemitones root
Let’s implement addSemitones:
module Note =
let addSemitones note semitones =
// find the index where the item of the list equals note
let index =
all
|> List.findIndex ((=) note)
// add the semitones to the index
// and get only the rest of the division
let newIndex = (index + semitones) % all.Length
all[newIndex]
and call this function in the notes function:
module MajorScale =
let notes (MajorScale root) =
intervals
|> List.take (intervals.Length - 1)
|> List.scan Note.addSemitones root
At the end of the script, we can print the notes of the scale:
// Add this helper on top of the file, just after the open statements
module String =
let joinWith (separator: string) (strings: string list) =
String.Join(separator, strings)
MajorScale randomNote
|> MajorScale.notes
|> List.map Note.toString
|> String.joinWith ", "
|> printfn "Notes of the major scale: %s"
// With randomNote = C, it prints:
// Notes of the major scale: C, D, E, F, G, A, B
Yay, now we can play random notes in this scale and it sound good!
Conclusion
That’s all for this step. You can check out the full code here.
Next step: Chords of the Major scale