Music theory in F# - Chords of the Major scale
This is the third part of the music theory in F# series:
- Introduction
- Step 1: Random note
- Step 2: The Major scale
- Step 3: Chords of the Major scale
Theory
Imagine, you found a good melody in C Major, great! It can be a good idea to have some chords around it.
First idea, you can play octaves on top of your melody, but play only notes in your scale.
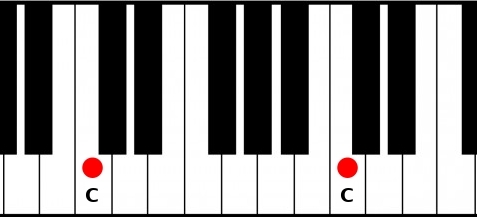
Octaves are OK but they feel a bit hollow. That’s OK if you want this kind of feeling in your song.
If you want some consistency, octaves may not be the best choice. Just add the fifth and your chord will gain some power! How do you create these power chords? Choose a note and add 7 semitones:
C power chord (also noted C5)
Root: C
Fifth: G (C + 7 semitones)
D5
Root: D
Fifth: A (D + 7 semitones)
...
These power chords are used a lot in rock, punk and metal.
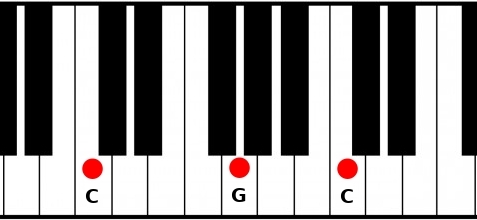
Power chords are great and powerful, but they miss something, we can’t say if they are joyful or sad. For that, add the third to your power chord.
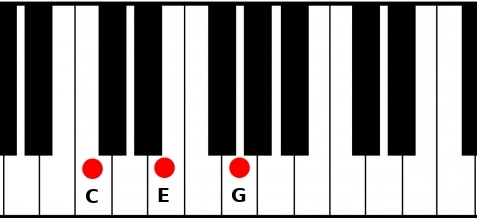
If the third is 4 semitones away from the root, this third is called major third, and the chord is a major chord. Major chords sounds joyful, they are noted with the name of the root. So the C chord is a C Major.
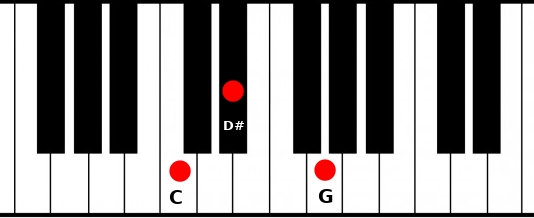
If the third is 3 semitones away from the root, this third is called minor third, and the chord is a minor chord. Minor chords sounds sad, they are noted with a little m. So Cm is a C minor.
Here are some examples:
C Major (C)
Root: C
Third: E (C + 4 semitones)
Fifth: G (C + 7 semitones)
C Minor (Cm)
Root: C
Third: D# (C + 3 semitones)
Fifth: G (C + 7 semitones)
A minor (Am)
Root: A
Third: C (A + 3 semitones)
Fifth: E (A + 7 semitones)
F# minor (F#m)
Root: F#
Third: A (F# + 3 semitones)
Fifth: C# (F# + 7 semitones)
OK, we know octaves, power chords, Major chords and minor chords, but can we play any chord we want on top of our song?
We can, but it will sound strange. If your melody is made with C, E and G and you play a C minor (made with C-D#-G) chord on it, you will play at the same time the E from your melody and the D# from your Cm chord. D# and E are just a semitone away frow each other, if you play them at the same time, it will sound really dissonant.
It is not forbidden, it can be also awesome to create a lot of tension.
A better option to avoid dissonance is to use only the notes of your scale.
- Choose one note of the scale as the chord root
- Add the third note of the scale from this chord root
- Add the fifth note of the scale from this chord root
C Major scale : C, D, E, F, G, A, B
The chord with a C root will be:
Root: C
Third: E (third note from the C)
Fifth: G (fifth note from the C)
There are 4 semitones between the C and the E, so the third is Major.
The C chord in a C Major scale is a C Major (noted C).
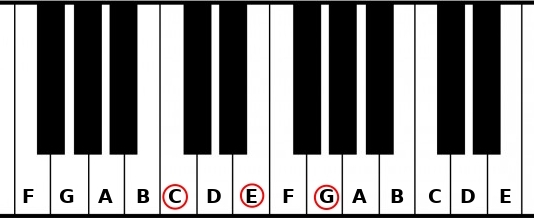
The chord with a D root will be:
Root: D
Third: F (third note from the D)
Fifth: A (fifth note from the D)
There are 3 semitones between the D and the F, so the third is Minor.
The D chord in a C Major scale is a D minor (noted Dm).
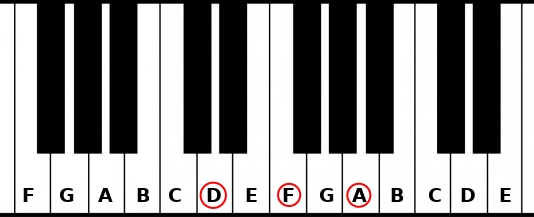
So in the C Major scale, you have these chords:
- C
- Dm
- Em
- F
- G
- Am
- ???
Beware of the 7th chord, it is special:
C Major scale : C, D, E, F, G, A, B
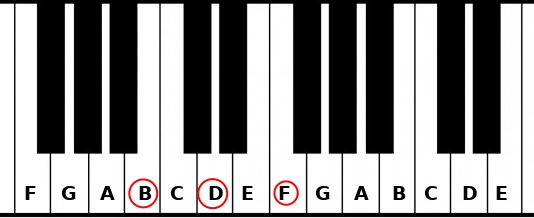
The chord with a B root will be:
Root: B
Third: D (third note from the B)
Fifth: F (fifth note from the B)
There are 3 semitones between the B and the D, so the third is minor.
BUT there are only 6 semitones between the B and the F,
the fifth is not perfect (7 semitones away from the root),
it is a diminished fifth.
The B chord in a C Major scale is a B diminished (B° or Bdim).
Diminished chords sounds weird because of this diminished fifth, they are spicy, uncomfortable. It is great if you want this feeling in your song, but I you don’t, you can avoid it.
Now we know all the chords of C Major:
- C
- Dm
- Em
- F
- G
- Am
- B°
We can generalize this to any Major scale, each position is called a degree and can be Major, minor or diminished. Major degree are upper case, minor and diminished degrees are lower case:
1. Major (noted I)
2. minor (noted ii)
3. minor (noted iii)
4. Major (noted IV)
5. Major (noted V)
6. minor (noted vi)
7. diminished (noted vii°)
For any Major scale, list all the notes in it and apply the chord type (Major, minor, diminished) of its corresponding degrees to find all the chords you can play:
E Major scale:
E, F#, G#, A, B, C#, D#
Chords:
| Degree | Chord | Root-Third-Fifth |
|--------|-------|------------------|
| I | E | E G# B |
| ii | F#m | F# A C# |
| iii | G#m | G# B D# |
| IV | A | A C# E |
| V | B | B D# F# |
| vi | C#m | C# E G# |
| vii° | D#° | D# F# A |
To build a chord progression, it is a good idea to start with the first degree and insist on it, the listener will understand that this chord is the root, it will feel like home. Then play any chord you want.
Example in C Major:
One more thing, these degrees are really important because some chords progressions work better than others, they are called cadences. Finishing your chord progression with the V degree and starting again with the I degree work really well. This is called a perfect authentic cadence. There are a lot of existing cadences.
One of the most known chord progression is the I-V-vi-IV
This was this progression in the famous Axis of awesome - 4 chords song.
Code
Chord
Just after the Note module, we’ll add the ChordType type:
type ChordType =
| Major
| Minor
| Diminished
module ChordType =
let fromIntervals intervals =
match intervals with
| [4; 7] -> Major
| [3; 7] -> Minor
| [3; 6] -> Diminished
| _ -> invalidOp "Unknown interval"
fromIntervals is a function that returns the ChordType depending on a list of intervals. Pattern matching works well with lists, so if there is intervals of 4 and 7 semitones, the chord is Major, and so on. We know only three types of chords so any other form of intervals will throw an InvalidOperationException. Exceptions may not be the best way to handle errors in a functional language but it is simpler to explain.
We could be more strict by modeling this way:
type ThirdType =
| MinorThird
| MajorThird
type FifthType =
| PerfectFifth
| DiminishedFifth
type ChordType =
| Major
| Minor
| Diminished
| MajorFlat5
// Tuple of ThirdType AND FifthType
type TriadType = ThirdType * FifthType
module ChordType =
let fromIntervals triadType =
match triadType with
| MajorThird, PerfectFifth -> Major
| MinorThird, PerfectFifth -> Minor
| MajorThird, DiminishedFifth -> MajorFlat5
| MinorThird, DiminishedFifth -> Diminished
It is more strict and there can’t be any error by design, but there are a lot more other chord types (Major 7, Minor 7, half diminished, sus2, sus4, inversions…). That’s why intervals is just a list of int and not a stricter type.
Let’s forgot this stricter approach a keep the code with the int list.
Now the Chord type. A chord is defined by the root Note and a ChordType.
// Just after ChordType
type Chord = Chord of Note * ChordType
module Chord =
let name (Chord (root, chordType)) =
let note = root |> Note.name
match chordType with
| Major -> note
| Minor -> $"{note}m"
| Diminished -> $"{note}°"
Chord is a single union-case, composed by a tuple of Note and ChordType.
The name function takes a Chord and deconstructs it to have access to the root and the chordType.
Degree
Degree implementation is very close to Chord because it is an abstraction of a chord in any major scale.
// Just after Chord
type DegreeName = I | II | III | IV | V | VI | VII
module DegreeName =
let all = [ I; II; III; IV; V; VI; VII ]
type Degree = Degree of DegreeName * ChordType
module Degree =
let name (Degree (degreeName, chordType)) =
let romanName = string degreeName
match chordType with
| Major -> romanName
| Minor -> romanName.ToLower()
| Diminished -> $"{romanName.ToLower()}°"
Chords of the scale
We don’t know how to implement it for now, but we know its signature:
module MajorScale =
// Other functions
let chords (scale: MajorScale): (Degree * Chord) list =
[]
// Expected behavior
let degreesAndChords =
MajorScale C
|> MajorScale.chords
let expectedContent =
[
I, Chord (C, Major)
II, Chord (D, Minor)
III, Chord (E, Minor)
IV, Chord (F, Major)
V, Chord (G, Major)
VI, Chord (A, Minor)
VII, Chord (B, Diminished)
]
We saw that the degrees of the Major scale are:
I, ii, iii, IV, V, vi, vii°
So we can zip the degrees with the notes of the scale:
module MajorScale =
// Other functions
let private degrees = [
Degree (I, Major)
Degree (II, Minor)
Degree (III, Minor)
Degree (IV, Major)
Degree (V, Major)
Degree (VI, Minor)
Degree (VII, Diminished)
]
let chords (scale: MajorScale): (Degree * Chord) list =
scale
|> notes
|> List.zip degrees
|> List.map (fun (degree, note) ->
let (Degree (_, chordType)) = degree
degree, Chord (note, chordType)
)
List.zip combine the first element of the two lists, then the second element of the two lists, and so on:
let numbers = [1; 2; 3]
let strings = [ "foo"; "bar"; "baz" ]
let zipped = List.zip numbers strings
let expected = [
1, "foo"
2, "bar"
3, "baz"
]
List.zip here will return a (Degree * Note) list. Then we have to map each tuple to return the Degree * Chord depending on the Note and on the ChordType of the Degree.
List.map takes a function 'a -> 'b and a 'a list and returns a 'b list. 'a and 'b are generic type and in F#, they start with a '.
let increment x = x + 1
// [2; 3; 4]
let incrementedNumbers =
[1; 2; 3]
|> List.map increment
List.zip returns a tuple, so the parameter of the lambda should be deconstructed by writing fun (degree, note) -> .... It means that this lambda takes one argument which is a deconstructed tuple.
For each tuple, we deconstruct the Degree to extract the ChordType and then we can return a Degree * Chord.
This List.zip followed by List.map can be refactored with List.map2:
module MajorScale =
// Other functions
let private degrees = [
Degree (I, Major)
Degree (II, Minor)
Degree (III, Minor)
Degree (IV, Major)
Degree (V, Major)
Degree (VI, Minor)
Degree (VII, Diminished)
]
let chords (scale: MajorScale): (Degree * Chord) list =
let degreeChord degree note =
let (Degree (_, chordType)) = degree
degree, Chord (note, chordType)
List.map2
degreeChord
degrees
(notes scale)
At the end of the script, we can print the chords of the scale:
// Show the chords of the scale
MajorScale randomNote
|> MajorScale.chords
|> List.iter (fun (degree, chord) ->
let degreeName = Degree.name degree
let chordName = Chord.name chord
printfn "%-4s: %s" degreeName chordName
)
List.iter executes a function for each element. To print Degree * Chord we use printfn with the %-4s which means:
it’s a string that takes exactly 4 characters and is left-aligned
Conclusion
That’s all for this step. You can check out the full code here.
Next step: Modes of the Major scale